In college, I faced an interesting problem in a geometry class: my professor had drawn a “tilted” parabola and asked us how to solve it. My initial thought was to manipulate the parabola’s equation directly to account for the tilt, but the approach we were taught was far more elegant: instead of rotating the parabola itself, we could rotate the entire coordinate system using linear algebra, which brought a new perspective on the solution. While we hadn’t formally covered this concept yet, it simplified the calculations and revealed a deeper connection between geometric transformations and linear algebra.
Consider a standard parabola $y = ax^2$. Observe that, if rotated, this parabola remains unchanged in shape, as if we’ve just “tilted our head”. Mathematically, this transformation can be expressed using a rotation matrix, $R(\theta)$:
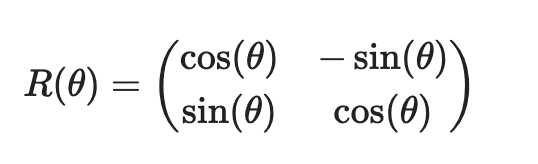
Here lies the elegance: by rotating the coordinate system by an angle $\theta$ , each point $(x, y)$ in the original system maps to a new point $(x{\prime}, y{\prime})$ in the rotated system via:
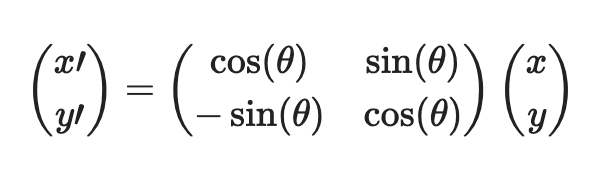
This transformation is orthogonal, which means that the inverse transformation is simply the transpose of the matrix. This property ensures that distances and angles are preserved — a crucial feature of rigid rotations. The inverse transformation, which is needed to express the rotated parabola in terms of the original coordinates, is:
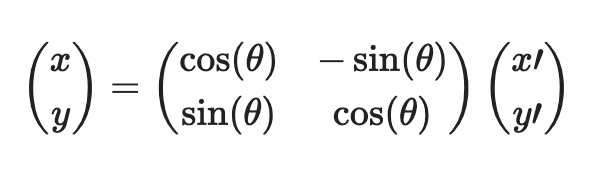
Applying this transformation to the parabola equation $y{\prime} = ax{\prime}^2$ produces a relationship in the original coordinates that defines the rotated parabola:
$\sin(\theta)x + \cos(\theta)y = a(\cos(\theta)x – \sin(\theta)y)^2$
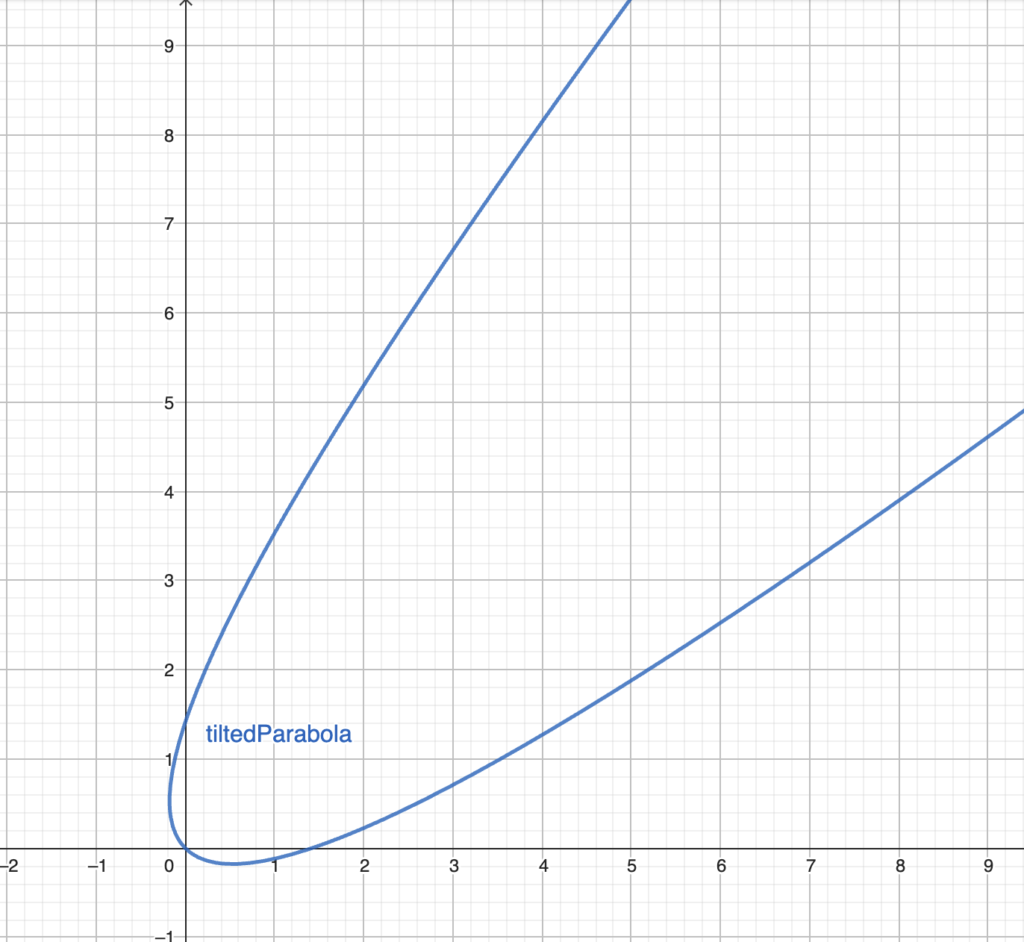
This final equation describes the same parabola, now viewed from a rotated angle. The parameter a continues to control the parabola’s width, while $\theta$ determines its orientation.
Here it is on GeoGebra:
Leave a Reply